Deep Learning을 공부하고자 하는 많은 입문자들을 위하여 내가 공부하면서 입문서로 가장 도움이 되었던 Michael Nielsen의 온라인 도서를 여기 장별로 정리하여 두고자 한다.
이 장에서 나오는 내용들은 그의 온라인 도서 2장에 대한 내용을 한국어로 얼기설기 번역한 것이다. 번역이 어색하지만, 개념을 이해하기에는 무리가 없다고 생각한다.
지난 장에서는 신경망이 경사 하강 알고리즘을 사용하여 가중치와 편향을 학습하는 방법을 살펴보았습니다. 그러나, 비용함수의 기울기를 계산하는 방법에 대해서는 다루지 않았습니다. 이번 장에서는 이러한 경사를 계산하는 빠른 알고리즘인 역전파 알고르즘에 대해서 알아보도록 하겠습니다.
역전파 알고리즘은 1970년대에 처음 소개되었지만, David Rumelhart, Geoffrey Hinton가 Ronald William이 1986년 유명한 논문을 발표하기 전까지 그 중요성이 제대로 인식되지 않았습니다. 이 논문에서는 역전파 알고리즘이 기존 학습 방식보다 훨씬 빠르게 작동하는 여러 신경망을 소개하며 이를 통해 이전에는 해결하기 어려웠던 문제들을 신경망을 통해 해결할 수 있게 되었습니다. 오늘날 역전파 알고리즘은 신경망 학습의 핵심으로 자리잡고 있습니다.
이 장은 책의 나머지 부분보다 수학적으로 더 깊이 있게 다룹니다. 수학에 별로 관심이 없다면 이 장을 건너 뛰어도 좋습니다.
역전파의 핵심은 비용함수 $C$의 어떤 가중치 $w$나 혹은 편향 $b$ 에 대하여 편미분 $\partial C / \partial w$ 한 것의 수학적 표현입니다. 이 표현식은 가중치와 편향을 변경할 때, 비용이 얼마나 빠르게 변하는지를 알려줍니다. 표현식은 다소 복잡하지만 각 요소가 자연스럽고 직관적인 해석을 제공한다는 점에서 매력적입니다. 따라서 역전파 알고리즘은 단순히 빠른 학습 알고리즘이 아닙니다. 실제로 가중치와 편향을 변경하면 네트워크의 전반적인 동작이 어떻게 변하는지에 대한 자세한 통찰력을 제공합니다. 이는 자세히 연구해볼 만한 가치가 있습니다.
다라서 이 장을 훝어 보거나 바로 다음 장을 넘어가고 싶으시다면 그것도 좋습니다. 역전파를 블랙박스처럼 다루더라도 책의 나머지 부분을 이해할 수 있도록 이 책은 구성되어 있습니다. 물론 이 책의 후반부에는 이 장의 결과를 다시 언급하는 부분도 있습니다. 하지만 모든 추론을 이해하지 못하더라도 그 부분에서는 주요 결론을 이해할 수 있을 것입니다.
개요: 신경망의 출력을 계산하기 위한 빠른 행렬 기반 접근 방법
역전파 알고리즘에 대해 논의하기 전에 신경망의 출력을 계산하는 빠른 행렬 기반 알고리즘을 먼저 살펴보도록 하겠습니다. 사실 이 알고리즘은 지난 장의 마지막 부분에서 간략하게 살펴보았습니다. 여기에서는 조금 더 상세하게 살펴보도록 하겠습니다. 이는 익숙한 맥락에서 역전파 알고리즘으로 접근하는 좋은 방법이기도 합니다.
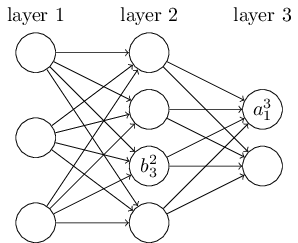
네트워크의 가중치를 명확하게 나타낼 수 있는 표기법부터 시작해보겠습니다. 우리는 ${w^l}_{jk}$를 $(l-1)$ 계층의 $k^{th}$ 뉴런에서 $l^{th}$ 계층의 $j^{th}$ 뉴런으로의 연결에 대한 가중치를 나타낸다고 정의하겠습니다. 예를 들어 아래 다이어그램은 네트워크의 두 번째 층의 네번째 뉴런에서 세 번째 층의 두 번째 뉴런으로 연결되는 연결의 가중치를 보여줍니다.
이 표기법은 처음에는 복잡하고 숙달되는데 약간의 노력이 필요합니다. 하지만, 조금만 노력하면 쉽고 자연스럽게 표기할 수 있습니다. 이 표기법의 한가지 이상한 점은 인덱스 $j$와 $k$의 순서입니다. 앞에 있는 인덱스 $j$가 입력쪽 뉴런을 나타내고 뒤에 이는 인덱스 $k$가 출력쪽 뉴런을 나타내는 것이 더 자연스럽다고 생각할 수 있습니다. 하지만, 그 반대로 표시한 이유가 있습니다. 그 이유에 대해서는 곧 살펴보도록 하겠습니다.
우리는 신경망의 편향과 활성화에 대해서도 비슷한 표기법을 사용할 것입니다. ${b^l}_j$은 $l^{th}$ 계층의 $j^{th}$ 뉴런의 편향을 의미합니다. 그리고 ${a^l}_j$는 $l^{th}$ 계층의 $j^{th}$ 뉴런의 활성화 값을 의미합니다. 아래 그림은 이를 설명하는 예제 그림입니다.
${a^l}_j$는 $(l-1)^th$ 계층의 모든 활성화 값들과 연관이 있는 $l^{th}$ 계층의 $j^{th}$ 뉴런의 활성화 값입니다. 이것은 다음의 식으로 계산할 수 있습니다. (마지막 장에서 이 식과 식 (4)의 비교에 대해서 설명하도록 하겠습니다.)
$a^{l}_j = \sigma\left( \sum_k w^{l}_{jk} a^{l-1}_k + b^l_j \right),\tag{23}$
이 식을 행렬을 이용하여 다시 작성하기 위하여 각 계층에 대한 가중치 행렬을 $w^l$이라고 정의하겠습니다. 가중치 행렬 $w^l$의 각 요소들은 뉴런의 $l^{th}$ 계층으로 연결된 가중치들입니다. 다시 말해, $j^{th}$ 행의 $k^{th}$ 열에 있는 요소가 ${w^l}_{jk}$입니다. 이와 유사한 방법으로 각 계층($l$)에 대한 편향 벡터 $b^l$을 정의할 수 있습니다. 편향 벡터의 요소들은 $l^{th}$ 계층의 각 뉴런에 대한 편향값, ${b^l}_j$를 의미합니다. 이는 활성화 벡터 $a^l$의 각 요소인 ${a^l}_j$도 마찬가지입니다.
식 (23)을 행렬 형태로 다시 작성하기 위해 마지막으로 필요한 것은 $\sigma$ 함수를 벡터화하는 것입니다. 이전 장에서 벡터화에 대하여 간략하게 살펴보았습니다. 함수의 벡터화란 특정 벡터 $v$의 모든 구성요소에 대하여 $\sigma$와 같은 함수를 적용하는 것입니다. 우리는 이렇게 적용하는 것을 $\sigma (v)$와 같이 표기했었습니다. 다시 말해, $\sigma (v)$의 요소들 ${\sigma(v)}_j = \sigma (v_j)$라는 뜻입니다. 예를 들어 $f(x) = x^2$과 같은 함수에 대하여 $f$의 벡터화된 형태는 다음과 같습니다.
$f\left(\left[ \begin{array}{c} 2 \\ 3 \end{array} \right] \right) = \left[ \begin{array}{c} f(2) \\ f(3) \end{array} \right] = \left[ \begin{array}{c} 4 \\ 9 \end{array} \right],\tag{24}$
이런 점들을 고려해서 식(23)을 아래와 같이 간략하게 다시 쓸 수 있습니다.
$a^{l} = \sigma(w^l a^{l-1}+b^l).\tag{25}$
이 표현은 한 계층의 활성화 값이 이전 계층의 활성화 값과 어떻게 연관되는지에 대해 훨씬 더 전체적인 시각을 제공해줍니다. 즉, 가중치 행렬을 활성화 행렬에 곱한(apply) 다음, 편향 벡터를 더해준 후에 마지막으로 $\sigma$ 함수를 적용하면 됩니다. 이러한 전체적인 시각은 지금까지 살펴본 뉴런 단위의 시각보다 훨씬 쉽고 간결하며 복잡한 인덱스를 신경쓰지 않아도 훨씬 쉽게 그 의미를 파악할 수 있도록 해줍니다. 이 표현식은 실제 구현시에도 유용한데 대부분 행렬 라이브러리가 행렬의 곱셈, 벡터 덧셈 벡터화를 빠르게 구현할 수 있는 방법을 제공하기 때문입니다. 실제로 지난 장의 코드들은 이 표현식을 암묵적으로 사용하였습니다.
식 (25)를 활용하여 $a^l$을 계산할 때, 함수 $\sigma$의 입력값(intermediate quantity) $z^l \equiv w^la^{l-1} + b^l$을 계산해야 합니다. 이 $z^l$을 우리는 $l$ 계층의 뉴런들에 대한 가중 입력(weighted input)이라고 부르도록 하겠습니다. 이 장에 후반에 이것이 어떻게 활용될 수 있는지 살펴보도록 하겠습니다. 식 (25)를 가중 입력 $z^l$을 이용하여 다시 쓰면, $a^l = \sigma (z^l)$과 같이 쓸 수 있습니다. 그리고 $z^l = {\sum}_k {w^l}_{jk}{a^{(l-1)}}_k + {b^l}_j$입니다. ${z^l}_j$는 $l$ 계층의 $j$ 뉴런에 대한 활성화 함수에 대한 가중 입력값입니다.
비용 함수에 대한 두가지 가정
역전파의 목적은 비용 함수 $C$의 가중치 $w$나 편향 $b$에 대한 편미분 $\partial C / \partial w$와 $\partial C / \partial b$을 계산하는 것입니다. 역전파가 제대로 작동하기 위해서는 비용함수의 형태에 대한 두가지 주요 가정을 해야합니다. 이러한 가정들에 대해서 설명하기 전에 먼저 비용함수의 예를 들어 생각해보도록 하겠습니다. 이전 장에서 언급한 바 있는 이차 비용함수 (식 (6))을 예로 다시 활용하도록 하겠습니다. 이전 절의 표기방법을 활용한, 이차 비용함수는 다음과 같습니다. ($n$은 모든 학습 데이터의 수를 나타내며, 총 합은 모든 학습 데이터, $x$에 대하여 수행하며, $y = y(x)$로 각 학습 데이터에 대한 우리가 추구하는 출력을 나타냅니다. $a^L = a^L(x)$는 입력 $x$에 대한 네트워크의 활성화된 출력 벡터를 의미합니다.)
$C = \frac{1}{2n} \sum_x \|y(x)-a^L(x)\|^2,\tag{26}$
자! 그렇다면, 우리는 역전파가 작동하게 하기 위하여 비용함수 $C$에 대한 어떤 가정을 해야할까요? 첫 번째 가정은 비용함수를 각 학습 데이터 $x$에 대한 각 비용 함수값 $C_x$의 평균 ($C = \frac{1}{n} \sum_x C_x$)으로 간주하는 것입니다. 이것을 우리가 예로 든 이차 비용함수에 적용하면, 개별 학습 데이터에 대한 비용은 $C_x = \frac{1}{2} \|y-a^L \|^2$와 같습니다. 이 가정은 이 책에서 다루는 모든 비용함수에도 적용됩니다.
이 가정이 필요한 이유는 역전파를 통해 실제로 할 수 있는 일이 각 학습데이터에 대한 편미분 $\partial C_x / \partial w$와 $\partial C_x / \partial b$을 계산하는 것이기 때문입니다. 그리고, 모든 학습 데이터에 대한 평균을 구함으로써 우리는 $\partial C / \partial w$와 $\partial C / \partial b$를 구할 수 있습니다.
두 번째 가정은 비용이 신경망 출력에 대한 함수라는 것입니다.
예를 들어, 이차 비용 함수에서의 비용은 각 학습 데이터 $x$에 대한 출력의 다음과 같은 함수임을 알 수 있습니다.
$C = \frac{1}{2} \|y-a^L\|^2 = \frac{1}{2} \sum_j (y_j-a^L_j)^2,\tag{27}$
물론 이 비용함수는 신경망의 출력뿐 아니라 우리가 바라는 출력값($y$, 답을 뜻함)에 따라 달라지기도 합니다. 비용을 우리가 바라는 출력값($y$)에 대한 함수로 간주하지 않는 이유는 그 출력값은 변수가 아니라 상수이기 때문입니다. 다시 말해, 개별 학습 데이터에 대한 답은 우리가 가중치와 편향을 조정한다고 바뀔 수 있는 값이 아닙니다. (주: 가중치와 편향을 조절하여 우리의 신경망의 출력이 우리가 바라는 답에 최대한 가깝도록 하는 것이 목표입니다.) 즉, 개별 학습 데이터에 대한 답은 신경망이 학습하는 것이 아닙니다. 따라서, $C$를 신경망의 활성화 출력(output activation) $a^L$에 대한 함수로 간주하고, $y$를 비용함수를 정의하는 (상수) 파라미터로 간주하는 것이 합리적입니다.
아다마르 곱셈 (Hadamard product, $s \odot t$)
역전파 알고리즘은 벡터의 덧셈, 벡터와 행렬의 곱셈 등 일반적인 선형대수 연산을 기반으로 합니다. 하지만 이러한 연산 중에 상대적으로 덜 사용하는 것이 있습니다. $s$와 $t$를 벡터라고 가정해 봅시다. 아다마르 곱셈이라고 알려진 $s \odot t$는 두 벡터의 요소를 곱하는 것입니다. $s \odot t$는 ${(s \odot t)}_j = s_jtj$를 뜻합니다. 예를 들면 아래와 같습니다.
$\begin{eqnarray} \left[\begin{array}{c} 1 \\ 2 \end{array}\right] \odot \left[\begin{array}{c} 3 \\ 4\end{array} \right] = \left[ \begin{array}{c} 1 * 3 \\ 2 * 4 \end{array} \right] = \left[ \begin{array}{c} 3 \\ 8 \end{array} \right].\tag{28}\end{eqnarray}$
이러한 요소별 곱셈을 아다마르 곱셈(Hadamard product) 또는 슈어 곱셈(Schur product)이라고 합니다. 여기서는 아다마르 곱셈이라고 부르겠습니다. 좋은 행렬 라이브러리는 일반적으로 아다마르 곱셈을 빠르게 구현할 수 있는 도구를 제공하는데, 이는 역전파를 구현하는데 유용합니다.
역전파 이론의 배경이 되는 4가지 기본 방정식
역전파는 네트워크의 가중치와 편향을 변경할 때 비용함수가 어떻게 변하는지 이해하는 것입니다. 궁극적으로 이는 $\partial C / \partial {w^l}_jk$와 $\partial C / \partial {b^l}_j$의 편미분을 계산하는 것을 의미합니다. 그러나 이를 계산하기 위해서 우리는 먼저 계산에 활용되는 매개값(intermediate quantity)인 ${\delta ^l}_j$를 도입해야 합니다. 우리는 이를 $l^{th}$ 계층의 $j^{th}$ 뉴런의 오류(error)라고 부르겠습니다.
역전파는 특정 뉴런에서의 오류값인 ${\delta ^l}_j$를 계산하는 절차를 제공해주며, 이를 바탕으로 $\partial C / \partial {w^l}_jk$와 $\partial C / \partial {b^l}_j$를 구할 수 있습니다.
오류가 어떻게 정의되는지 이해하기 위해 우리의 신경망 내에 작은 악마가 존재한다고 가정해보겠습니다.
위 그림에서 우리의 작은 악마는 $l$ 계층의 $j^{th}$ 뉴런에 앉아 있습니다. 그 뉴런으로 입력들이 들어올 때, 악마는 뉴런의 작동에 훼방을 놓습니다. 악마는 뉴런의 가중 입력값에 작은 변화를 $\Delta {z^l}_j$를 추가합니다. 그 결과 뉴런은 출력으로 $\sigma ({z^l}_j)$를 내놓는 대신 $\sigma ({z^l}_j + \Delta {z^l}_j)$를 출력으로 내놓습니다. 이 변화는 우리의 신경망의 이후 계층들을 따라 전파되어 결국에는 전체적인 비용이 $\frac{\partial C}{\partial z^l_j} \Delta z^l_j$만큼 변하게 만듭니다.
자, 이제 우리의 작은 악마가 우리를 돕고 있다고 가정해봅시다. 이것은 다시 말하자면 전체 비용을 줄여줄 수 있는 $\Delta {z^l}_j$를 찾기 위해 노력한다는 것을 의미합니다. $\frac{\partial C}{\partial z^l_j}$이 양수던 음수이던 큰 절대값을 갖는다고 가정해봅시다. 그렇다면, 우리의 악마는 $\frac{\partial C}{\partial z^l_j}$와 반대 부호를 갖는 $\Delta {z^l}_j$를 선택함으로써 비용을 조금이라도 낮출 수 있습니다. 반대로, $\frac{\partial C}{\partial z^l_j}$이 0에 가까운 값을 가진다고 가정해봅시다. 그렇다면 가중 입력값 ${z^l}_j$의 값을 교란한다고 해서 전체적인 비용을 증가시키거나 할 수 없을 것입니다. 그렇다면 우리의 작은 악마가 아는 한, 그 뉴런은 이미 최적에 가깝다고 할 수 있을 것입니다. 즉, $\frac{\partial C}{\partial z^l_j}$으로 그 뉴런에서 오류를 어림짐작(heuristic sense)할 수 있습니다.
이 논의를 조금 더 이어나가, 우리는 $l$ 계층의 $j$ 뉴런의 오류를 ${\delta ^l}_j$라고 정의하겠습니다.
$\begin{eqnarray} \delta^l_j \equiv \frac{\partial C}{\partial z^l_j}.\tag{29}\end{eqnarray}$
우리는 지금까지의 관례대로, $\delta ^l$을 $l$ 계층에서의 오류를 나타내는 벡터를 의미한다고 하겠습니다. 역전파는 모든 계층에서 $\delta ^l$를 계산할 수 있는 방법을 제공합니다. 그리고, 이들을 이용해서 우리는 최종적으로 우리가 구하고자 하는 $\partial C / \partial {w^l}_{jk}$와 $\partial C / \partial {b^l}_j$를 계산할 수 있습니다.
우리의 작은 악마가 가중 입력 ${z^l}_j$를 변화시키는 이유에 대해 궁금해할 수 있습니다. 당연하겠지만, 악마는 그 뉴런의 활성화 출력 (output activation) ${a^l}_j$를 변경시키는 것이 더 자연스러울 수 있습니다. 만약 그렇게 한다면, 우리는 오류를 $\frac{\partial C}{\partial {a^l}_j}$와 같이 계산할 수 있을 것입니다. 이렇게 해도 우리는 이후 논의를 유사하게 이어나갈 수 있습니다. 하지만 이렇게 한다면 역전파에 기술이 대수적으로 조금 더 복잡해집니다. 따라서 우리는 우리의 오류 측정을 우리의 원래 방법대로 ${\delta ^l}_k = \frac{\partial C}{\partial {z^l}_j}$와 같이 하도록 하겠습니다.
공격 계획: 역전파는 네 가지 기본 방정식을 기반으로 합니다. 이 방정식들을 함께 사용하면 오차 $\delta ^l$와 비용함수의 기울기를 계산할 수 있습니다. 지금부터 그 네 가지 방정식을 살펴보도록 하겠습니다. 하지만, 이 방정식들을 바로 이해할 수 있을 것이라고 기대해서는 안됩니다. 기대가 큰 만큼 실망도 커지기 쉽습니다. 사실 역전파 방정식은 매우 심오해서 방성식을 깊이 파고들수록 이를 제대로 이해하려면 상당한 시간과 인내가 필요합니다. 하지만 그 인내의 열매는 매우 달콤합니다. 따라서 이 섹션의 논의는 이를 위한 첫 걸음에 불과하며, 이해를 위한 도움이 되길 바라겠습니다.
이 장의 후반부에서는 각 방정식들에 대한 이해를 돕기 위해서 간략한 증명을 해보도록 하겠습니다. 그리고, 이 방정식을 알고르즘 형태의 유사(혹은 의사)코드(pseudocode)를 작성해보고, 이들을 실제 작동하는 Python 코드로 실행해보도록 하겠습니다. 그리고, 마지막 부분에서는 역전파 방정식의 직관적 의미와 역전파 방정식들이 어떻게 개발되었는지에 대해서 논의하도록 하겠습니다. 이 과정을 통해서 우리는 네 가지 기본 방정식들을 여러 번 다시 다루게 될 것이며, 이들에 대한 이해가 깊어짐에 따라 이들이 어쩌면 아름답고 자연스럽게 보일 것입니다.
출력 계층의 오류를 위한 방정식, $\delta ^L$
$\delta ^L$은 다음과 같이 기술할 수 있다.
$\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j).\tag{BP1}\end{eqnarray}$
이 수식은 매우 자연스럽다. 이 식의 첫 번째 우변인 $\partial C / \partial {a^L}_j$는 $j^{th}$ 활성화 출력의 함수로써 비용이 얼마나 빠르게 변화하는지에 대한 것입니다. 예를 들어, 비용이 특정 출력 뉴런 $j$의 영향을 많이 받지 않는다면 ${\delta ^L}_j$는 작을 것이라고 예상할 수 있습니다. 두 번째 우변, $\sigma' ({z^L}_j)$은 ${z^L}_j$에 대하여 활성화 함수 $\sigma$가 얼마나 빠르게 변화하는지에 대한 것입니다.
식 (BP1)의 모든 요소들은 빠르게 계산할 수 있습니다. 특히 신경망의 행동을 계산하면서 ${z^L}_j$를 계산할 수 있습니다. 그리고, $\sigma' ({z^L}_j)$도 추가적인 약간의 계산으로 산출해낼 수 있습니다. $\partial C / \partial {a^L}_j$의 정확한 형태는, 당연하게도, 비용함수의 형태에 영향을 받습니다. 그러나, 비용함수가 알려져 있다면, $\partial C / \partial {a^L}_j$을 계산하는 것은 큰 문제가 되지 않습니다. 만약 우리가 이차 비용함수, $C = \frac{1}{2} \sum_j (y_j-a^L_j)^2$,를 사용한다면, 그 편미분 방정식은, 당연하겠지만, $\partial C / \partial a^L_j = (a_j^L-y_j)$가 됩니다.
식 (BP1)은 $\delta ^L$에 대한 요소별 표현식입니다. 그러나 이것은 우리가 역전파에서 필요한 행렬 기반의 형태는 아닙니다. 이를 행렬 기반의 수식으로 다음과 같이 쓸 수 있습니다.
$\begin{eqnarray} \delta^L = \nabla_a C \odot \sigma'(z^L).\tag{BP1a}\end{eqnarray}$
$\nabla_a C$는 편미분 $\partial C / \partial {a^L}_j$을 구성요소로 갖는 벡터입니다. $\nabla_a C$은 활성화 출력에 대한 C의 변화률로 이해할 수 있습니다. 식 (BP1a)와 식 (BP1)이 동일하다는 것은 어렵지 않게 파악할 수 있습니다. 따라서 지금부터 식 (BP1)이라고 하는 것은 이 두 식을 모두 뜻하는 것으로 사용하겠습니다. 우리가 예로 사용하고 있는 이차 비용함수, $\nabla_a C = (a^L - y)$를 식 (BP1)처럼 행렬 형태로 기술하면 다음과 같은 식이 됩니다.
$\begin{eqnarray} \delta^L = (a^L-y) \odot \sigma'(z^L).\tag{30}\end{eqnarray}$
이 식의 모든 구성요소들은 벡터 형태로 되어있으며, Numpy와 같은 라이브러리로 쉽게 계산될 수 있습니다.
다음 계층의 오류, $\delta ^{l+1}$에 대한 오류 방정식 $\delta ^l$
$\begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l),\tag{BP2}\end{eqnarray}$
$(w^{l+1})^T$는 $(l+1)^{th}$ 계층에서의 가중치 행렬 $w^{l+1}$의 전치 행렬을 의미한다. 위 식은 복잡해 보이기는 하나, 각 요소들의 의미는 명확합니다. ${l + 1}^{th}$ 계층에 대한 오류 $\delta ^ {l+1}$을 알고 있다고 가정해봅시다. 가중치 행렬의 전치 행렬($(w^{l+1})^T$)을 적용하는 것은 신경망을 통해 오류를 뒤로 이동시켜 $l^{th}$ 계층의 출력에서 오류를 측정하는 것으로 직관적으로 간주할 수 있습니다. 그리고 난 후, 아다마르 곱셈 ($\odot \sigma' (z^l)$)을 적용합니다. 이것은 오류를 $l$ 계층의 활성화 함수로 옮겨, $l$ 계층의 가중 입력에서의 오류 $\delta ^l$을 산출해 줍니다.
식 (BP1)에 식 (BP2)를 적용하여 우리는 신경망의 어떤 특정 계층에서의 오류 $\delta ^l$를 계산할 수 있습니다. 식 (BP1)을 이용하여 $\delta ^L$을 계산하고, 다시 식 (BP2)를 이용하여 $delta ^ {L-1}$을 계산합니다. 그리고, 식 (BP2)를 또 다시 이용하여 $\delta ^{L-2}$를 계산합니다. 이러한 방식으로 우리는 신경망 전체를 거꾸로 거슬러 갈 수 있습니다.
네트워크의 편향에 따른 비용 변화율에 대한 방정식
$\begin{eqnarray} \frac{\partial C}{\partial b^l_j} = \delta^l_j.\tag{BP3}\end{eqnarray}$
여기서 오류 ${\delta ^l}_j$는 $\partial C / \partial {b^l}_j$의 변화율과 정확히 같습니다. 이것은 좋은 소식입니다. 식 (BP1)과 식 (BP2)을 통해 우리는 ${\delta ^l}_j$를 계산하는 방법을 이미 알고 있습니다. 따라서 우리는 식 (BP3)을 아래와 같이 다시 쓸 수 있습니다.
$\begin{eqnarray} \frac{\partial C}{\partial b} = \delta,\tag{31}\end{eqnarray}$
네트워크의 모든 가중치에 대한 비용 변화율에 대한 방정식
$\begin{eqnarray} \frac {\partial C}{\partial {w^l}_{jk}} = {a^{l-1}}_k \delta^l_j.\tag{BP4}\end{eqnarray}$
이 식은 우리가 이미 어떻게 계산할지 알고 있는 $\delta ^l$과 $a^{l-1}$을 가지고 편미분 값인 $\partial C / \partial w^j_{jk}$를 계산하는 방법을 알려줍니다. 이 식을 조금 더 알기 쉽게 쓰면 아래와 같습니다.
$\begin{eqnarray} \frac{\partial C}{\partial w} = a_{in}\delta_{out},\tag{32}\end{eqnarray}$
이 식에서 $a_{in}$은 가중치에 대한 뉴런의 입력의 활성도이고, $\delta_{out}$은 가중치 $w$로 부터 뉴런의 출력 오류입니다. 이것을 가중치 $w$와 두 뉴런 사이의 연결 관점에서 조금 상세하게 들여다보면, 아래와 같음을 알 수 있습니다.
식 (32)에서 만약 활성화 입력값 $a_{in}$이 거의 0에 가까운 작은 값($a_{\rm in} \approx 0$)이라면, 기울기인 $\partial C / \partial w$도 작은 값일 것입니다. 이러한 경우 그 가중치로 인한 학습률은 낮다(느리게 학습한다)는 것을 뜻합니다. 즉, 경사 하강법을 적용하는 동안 가중치가 많이 변하지 않는다는 것입니다. 다시 말해, 식 (BP4)의 한가지 결과는 뉴런의 낮은 활성도로 인하여 학습률이 낮다는 것을 의미합니다.
식 (BP1)에서 (BP4)로 부터 이와 유사한 다른 통찰력을 얻을 수 있습니다. 출력 계층부터 살펴보도록 하겠습니다. 식 (BP1)의 $\sigma'(z^L_j)$ 부터 고려해보도록 하겠습니다. 이전 장에서 살펴본 바 있는 $\sigma(z^L_j)$가 0이나 1에 가까워질 때, 평평해지는 시그모이드(sigmoid) 함수의 그래프를 떠올려 봅시다. 함수가 평평해진다는 의미는 기울기는 0에 가까워진다는 뜻입니다. 다시말해, 이때 $\sigma'(z^L_j) \approx 0$이 됩니다. 즉, 여기서 우리가 얻을 수 있는 교훈은 이렇습니다. 만약 출력 뉴런이 낮은 활성도를 갖거나($\approx 0$) 높은 활성도를 가질($\approx 1$) 경우 출력 계층에서의 가중치는 낮은 학습율을 갖게 한다. 이 경우 출력 뉴런이 포화 상태에 도달했고, 그 결과 가중치가 학습을 멈추었거나, 느리게 학습하고 있다고 말하는 것이 일반적입니다. 출력 뉴런의 편향에도 비슷한 설명이 적용됩니다.
이전 계층에 대해서도 유사한 통찰력을 얻을 수 있습니다. 식 (BP2)의 $\sigma'(z^l)$을 한번 봅시다. 이것은 뉴런이 포화 상태일때 $\delta^l_j$이 작아짐을 뜻합니다. 즉, 포화된 뉴런에 입력되는 모든 가중치는 느리게 학습됩니다.
요약하면, 입력 뉴런이 낮은 활성화 상태에 있거나 출력 뉴런이 포화상태, 즉 높거나 낮은 활성화 상태가 되면 가중치가 느리게 학습됩니다.
이러한 관찰 결과는 그다지 놀랍지 않습니다. 그럼에도 불구하고 이러한 관찰 결과는 신경망이 학습하는 과정에 대한 우리의 이해도(mental model)를 개선하는 데 도움이 됩니다. 더 나아가 이러한 추록 방식을 바꿀 수 있습니다. 네 가지 기본 방정식은 표준 시그모이드 함수뿐만 아니라 모든 활성화 함수에 대해서도 적용할 수 있습니다. (곧 살펴보겠지만, 이 방정식들을 증명할 때, 시그모이드 함수의 특별한 속성이 관여하는 것이 아니기 때문입니다.) 따라서, 이들 방정식의 특성을 이용하여 특정 학습 특성을 갖는 활성화 함수를 설계할 수 있습니다. 예를 들어 (시그모이드가 아닌) $sigma'$이 항상 양수이고 함수값이 0에 가까워지지 않는 활성화 함수 $\sigma$를 선택한다고 가정해보겠습니다. 이러한 활성화 함수는 보통의 시그모이드 뉴런이 포화상태가 될 때, 학습률이 낮아지는 것을 방지할 수 있습니다. 이 책의 후반부에서 활성화 함수에 이러한 수정을 적용하는 예를 살펴보겠습니다. 네 가지 식 (BP1)부터 (BP4)를 염두해 두면 이러한 수정이 시도되는 이유와 그 영향을 이해하는데 도움이 될 수 있습니다.
이제 네 개의 기본 방정식 (BP1) ~ (BP4)를 증명해 보겠습니다. 네 개 모두 다변수 미적분학의 연쇄 법칙의 결과입니다. 연쇄 법칙에 익숙하다면 계속 읽기 전에 미분을 시도해 보시기를 강력히 권장합니다.
출력 오류, $\delta ^L$에 대한 표현식인 식 (BP1)부터 시작해 보겠습니다. 이 식을 증명하기 전에, 출력 오류를 다음과 같이 정의했던 것을 상기해보시기 바랍니다.
$\begin{eqnarray} \delta ^L_j = \frac{\partial C}{\partial z^L_j}.\tag{36}\end{eqnarray}$
합성함수 미분법(chain rule)을 적용하여 위의 편미분 식을 활성화 출력에 대한 편미분으로 아래와 같이 다시 표현할 수 있습니다. (여기서 합산은 출력 계층에 있는 모든 뉴런 $k$에 대한 것입니다.)
\begin{eqnarray} \delta^L_j = \sum_k \frac{\partial C}{\partial a^L_k} \frac{\partial a^L_k}{\partial z^L_j},\tag{37}\end{eqnarray}
물론, $k^{th}$ 뉴런의 출력 활성화는 $k = j$인 경우 $j^{th}$ 뉴런에 대한 가중 입력 $z^L_j$에 전적으로 의존합니다. 그리고, $k \neq j$인 경우 $\partial a^L_k / \partial z^L_j$는 사라지게 됩니다. 결론적으로 위 식은 아래와 같이 단순하게 쓸 수 있습니다.
$\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \frac{\partial a^L_j}{\partial z^L_j}.\tag{38}\end{eqnarray}$
그리고, $a^L_j = \sigma (z^L_j)$를 다시 떠올려 봅시다. 그러면, 위 식의 우변은 $\sigma'(z^L_j$로 다시 쓸 수 있습니다. 그러면 위 식은 아래와 같이 다시 쓸 수 있습니다. 그리고 그 식은 식 (BP1)과 같습니다.
$\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j),\tag{39}\end{eqnarray}$
다음으로 식 (BP2)를 증명해보겠습니다. 이 식은 $l$ 계층의 오류 $\delta ^l$에 대한 식을 다음 계층인 $l + 1$ 계층의 오류로 기술한 것입니다. 이를 위하여 우리는 $\delta ^l_j = \partial C / \partial z^l_j$를 $\delta ^{l+1}_j = \partial C / \partial z^{l+1}_k$를 이용해서 다시 써야합니다. 우리는 이 작업을 위하여 합성함수 편미분법(chain rule)을 사용할 것입니다. 식 (42)는 식 (41)의 우변에 있는 두 요소의 자리를 바꾸고, $\delta ^{l+1}_j$의 정의를 대입한 것입니다.
$\begin{eqnarray} \delta^l_j = \frac{\partial C}{\partial z^l_j} \tag{40}\\ = \sum_k \frac{\partial C}{\partial z^{l+1}_k} \frac{\partial z^{l+1}_k}{\partial z^l_j} \tag{41}\\ = \sum_k \frac{\partial z^{l+1}_k}{\partial z^l_j} \delta^{l+1}_k,\tag{42}\end{eqnarray}$
식 (42)의 첫번째 요소를 평가하기 위해서, 다음을 참고해보시기 바랍니다.
$\begin{eqnarray} z^{l+1}_k = \sum_j w^{l+1}_{kj} a^l_j +b^{l+1}_k = \sum_j w^{l+1}_{kj} \sigma(z^l_j) +b^{l+1}_k.\tag{43}\end{eqnarray}$
이것을 미분하면 아래와 같은 식을 얻을 수 있습니다.
$\begin{eqnarray} \frac{\partial z^{l+1}_k}{\partial z^l_j} = w^{l+1}_{kj} \sigma'(z^l_j).\tag{44}\end{eqnarray}$
이것을 식 (42)에 대입하면 아래와 같은 식을 얻을 수 있습니다. 그리고, 이것은 식 (BP2)와 같습니다.
$\begin{eqnarray} \delta^l_j = \sum_k w^{l+1}_{kj} \delta^{l+1}_k \sigma'(z^l_j).\tag{45}\end{eqnarray}$
이제 남은 것은 식 (BP3)과 (BP4)만 남았습니다. 이 두 방정식 역시 위의 두 방정식과 유사하게 합성함수 미분법을 적용하여 증명할 수 있습니다. 이 두 식을 증명하는 것은 연습문제로 남겨두도록 하겠습니다.
이것으로 역전파의 네 가지 기본 방정식에 대한 증명을 마무리하도록 하겠습니다. 증명이 복잡해 보일 수 있지만, 실제로는 합성함수 미분법을 신중하게 적용한 결과일 뿐입니다. 좀 더 간결하게 말하면, 역전파는 다변수 미적분학의 합성함수 미분법을 체계적으로 적용하여 비용 함수의 기울기를 계산하는 방법이라고 생각할 수 있습니다. 역전파에 대한 내용은 여기에서 마치도록 하겠습니다.
역전파 알고리즘
역전파 방정식은 비용 함수의 기울기를 계산하는 방법입니다. 이를 알고리즘 형태로 표현해보도록 하겠습니다.
- 입력 $x$: 입력 계층에 활성도 $a^1$을 설정한다.
- 순전파: 각 계층 $l = 2, 3, ..., L$에 대하여 $z^l = w^la^{l-} + b^l$과 $a^l = \sigma(z^l)$을 계산한다.
- 출력 오류 $\delta ^L$: $\delta ^L = \nabla_a C \odot \sigma'(z^L)$을 계산한다.
- 오류에 대한 역전파: 각 계층 $l = L - 1, L - 2, ..., 2$에 대하여 $\delta^{l} = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^{l})$를 계산한다.
- 출력: 오류 함수에 대한 기울기를 $\frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j$와 $\frac{\partial C}{\partial b^l_j} = \delta^l_j$로 계산한다.
이 알고리즘을 살펴보면 왜 역전파라고 불리는지를 알 수 있습니다. 오류 벡터 $\delta ^l$을 마지막 계층에서 시작해서 역으로 계산해가기 때문입니다. 신경망을 역방향으로 되짚어가며 계산한다는 것이 이상해 보일 수 있습니다. 하지만 역전파의 증명을 생각해보면 역방향으로 이동하는 것은 비용이 신경망의 출력의 함수라는 사실에 기인합니다. 이전 가중치와 편향에 따라 비용이 어떻게 달라지는지 이해하기 위하여 우리는 합성함수 편미분법을 반복적으로 적용하여 계층을 역방향으로 진행하며 네 가지 기본식들을 도출했습니다.
역전파를 위한 코드
역전파를 수학적으로 이해했으므로, 이제 이전 장에서 연전파를 구현하는데 사용했던 코드를 이해할 수 있습니다. 이 코드는 Network 클래스의 update_mini_bach 및 backprop 메서드에 포함되어 있습니다. 이 메서드의 코드들은 위에서 설명한 알고리즘을 그대로 구현한 것입니다. 특히 update_mini_batch 메서드는 현재 학습 예제의 미지배치에 대한 기울기를 계산하여 Netwrok의 가중치와 편향을 업데이트 합니다.
class Network(object):
...
def update_mini_batch(self, mini_batch, eta):
"""Update the network's weights and biases by applying
gradient descent using backpropagation to a single mini batch.
The "mini_batch" is a list of tuples "(x, y)", and "eta"
is the learning rate."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]대부분의 작업은 $\partial C_x / \partial b^l_j$와 $\partial C / \partial w^l_{jk}$편미분을 계산하기 위해 역전파 방법을 사용하는 delta_nabla_b, delta_nabla_w = self.backprop(x, y)라인에 의해 수행됩니다. 이 역전파 기법은 위에서 설명한 알고리즘을 면밀히 따릅니다. 한가지 다른 점은 각 계층을 인덱싱하는 방법입니다. 이것은 Python의 기능 중 음수 리스트 인덱스를 활용하여 리스트를 끝에서 부터 역방향으로 계산하는 기능을 활용하기 위한 것입니다. 역전파 기법의 코드는 다음과 같으며 $\sigma$와 이에 대한 미분 $\sigma'$와 비용 함수를 계산하는데 사용되는 몇몇 함수들도 함께 있습니다.
class Network(object):
...
def backprop(self, x, y):
"""Return a tuple "(nabla_b, nabla_w)" representing the
gradient for the cost function C_x. "nabla_b" and
"nabla_w" are layer-by-layer lists of numpy arrays, similar
to "self.biases" and "self.weights"."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# feedforward
activation = x
activations = [x] # list to store all the activations, layer by layer
zs = [] # list to store all the z vectors, layer by layer
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# backward pass
delta = self.cost_derivative(activations[-1], y) * \
sigmoid_prime(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
# Note that the variable l in the loop below is used a little
# differently to the notation in Chapter 2 of the book. Here,
# l = 1 means the last layer of neurons, l = 2 is the
# second-last layer, and so on. It's a renumbering of the
# scheme in the book, used here to take advantage of the fact
# that Python can use negative indices in lists.
for l in xrange(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
...
def cost_derivative(self, output_activations, y):
"""Return the vector of partial derivatives \partial C_x /
\partial a for the output activations."""
return (output_activations-y)
def sigmoid(z):
"""The sigmoid function."""
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
"""Derivative of the sigmoid function."""
return sigmoid(z)*(1-sigmoid(z))
역전파 알고리즘은 어떤 면에서 빠른 알고리즘일까?
역전파 알고리즘이 빠른 알고리즘이라는 것은 어떤 의미일까요? 이 질문에 대답하기 위하여 기울기 계산에 대한 다른 접근법을 생각해 보겠습니다. 신경망 연구의 초기 시절을 상상해 보세요. 아마 1950년대나 1960년대였을 것입니다. 세계 최초로 경사 하강법을 사용하여 학습하는 방법을 생각해낸 사람이 있습니다. 하지만, 이 아이디어를 실현하려면 비용함수의 기울기를 계산하는 방법이 필요합니다. 미적분학에 대한 지식을 떠올리며 합성함수 미분법을 사용하여 기울기를 계산할 수 있는지 확인해보기로 합니다. 하지만 조금 시도해본 후 대수학이 복잡해 보여 낙담하게 됩니다. 그래서 다른 접근법을 찾아보기로 합니다. 비용을 오롯이 가중치에 대한 함수 $C = C(w)$로 생각하기로 합니다. (편향에 대해서는 곧 다시 이야기하겠습니다.) 그리고, 가중치에 대하여 $w_1, w_2, ..$와 같이 번호를 매기고 특정 가중치 $w_j$에 대하여 $\partial C / \partial w_j$를 계산하고자 합니다. 이를 계산하기 위한 간단한 방법으로 다음의 어림을 사용합니다. (여기서 $\epsilon > 0$인 작은 양수이며, $e_j$는 $j^{th}$ 연결에 대한 단위 벡터입니다.)
$\begin{eqnarray} \frac{\partial C}{\partial w_{j}} \approx \frac{C(w+\epsilon e_j)-C(w)}{\epsilon},\tag{46}\end{eqnarray}$
이것은 다시 말해 두가지 약간 다른 $w_j$의 값에 대한 비용 C를 계산하여 이를 식 (46)에 대입하여 $\partial C / \partial w$를 어림할 수 있다는 뜻입니다. 같은 방법을 사용하여 우리는 편향 $b$에 대한 편미분인 $\partial C / \partial b$를 계산할 수 있습니다.
이 접근법은 매우 유용합니다. 개념적으로 간단하고 몇 줄의 코드만으로 구현할 수도 있습니다. 합성함수 편미분법을 사용하여 기울기를 계산하는 것보다 훨씬 쉽습니다.
안타깝게도 이 접근법이 유용하긴 해도 실제로 코드로 구현해보면 매우 느립니다. 그 이유를 이해하기 위해 신경망에 백만 개의 가중치가 있다고 가정해보겠습니다. 그러면, $\partial C / \partial w_j$를 계산하기 위하여, 각 개별적인 가중치 $w_j$에 대하여 $ C(w + \epsilon e_j)$를 계산해야합니다. 이는 기울기를 계산하기 위해 비용함수를 백만번 계산해야 하며, 이는 훈련 예제당 네트워크를 백만번 순방향으로 훝어야 한다는 것을 의미합니다. 우리는 $C(w)$도 계산해야하므로, 총 네트워크를 백만번 하고도 한번 더 훝어야 합니다.
역전파의 뛰어난 점은 모든 편미분 $\partial C / \partial w_j$을 동시에 계산할 수 있다는 것입니다. 이를 계산하기 위해 단지 순방향으로 네트워크를 한번 훑고 나서, 반대방향으로 다시 한번 훑으면 됩니다. 대략 역방향으로 훑는 계산 비용이나 순방향으로 훑는 계산 비용은 거의 같습니다. 따라서 역전파의 총비용은 신경망을 순방향으로 훑는 것을 두 번하는 것과 거의 같습니다. 이를 식 (46)에 기반한 접근법에 필요한 신경망을 백만 하고도 한번 더 훑는 것과 비교해 보시기 바랍니다. 따라서, 역전파가 식 (46)에 기반한 접근법보다 표면적으로 더 복잡해 보이지만 실제로 훨씬 더 빠릅니다.
이러한 속도의 향상은 1986년에 처음으로 완전히 실현되었으며, 신경망이 해결할 수 있는 문제의 범위를 크게 확장시켰습니다. 이로 인해 신경망을 사용하는 사람들이 급증했습니다. 물론 역전파 알고리즘이 만병통치약은 아닙니다. 1980년대 후반에도 사람들은 한계에 부딪혔는데, 특히 역전파 알고리즘을 사용하여 심층 신경망(여러개의 은닉층을 가진 신경망)을 훈련시키려고 할때 더더욱 그랬습니다. 이 책의 후반부에서는 현대의 컴퓨터와 몇 가지 기발한 새로운 아이디어들이 어떻게 역전파 알고리즘을 사용하여 이러한 심층 신경망을 훈련시키는지 살펴보겠습니다.
역전파: 전반적인 그림
역전파 알고리즘은 두 가지 풀리지 않는 미스터리를 가지고 있습니다. 첫째, 이 알고리즘은 실제로 무엇을 하는 것일까요? 우리는 출력에서 역전파되는 오류의 그림도 그려보았습니다. 하지만 더 깊이 파고들어 행렬과 벡터 곱셈을 할때 무슨 일이 일어나는지에 대한 직관력을 키울 수 있을까요? 두 번째 미스터리는 역전파 알고리즘은 어떻게 처음 발견되었을까요? 알고리즘의 단계를 따르거나 알고리즘이 작동한다는 증명을 따르는 것은 이와는 다른 별개의 문제입니다. 하지만 그렇다고 해서 문제를 잘 이해해서 알고리즘을 처음 발견할 수 있다는 의미는 아닙니다. 역전파 알고리즘을 발견하게 된 그렇듯한 추론이 있을까요? 이번 절에서는 이들 미스터리에 대해서 다루도록 하겠습니다.
알고리즘이 무엇을 하는지에 대한 직관을 향상시키기 위해 우리가 신경망에 있는 특정 가중치 $w^l_{jk}$에 작은 변화 $\Delta w^l_{jk}$를 가했다고 상상해봅시다.
이 가중치의 변화는 해당 뉴런의 출력 활성화에 변화를 일으킵니다.
그리고, 이 변화는 다음 계층의 모든 활성화에 영향을 미칩니다.
이러한 변경사항은 다음 계층에 변경을 일으키고, 그 다음 계층에서도 변경을 일으키며, 이런 식으로 최종 계층에서 변경을 일으키고 결국 비용함수에도 변경을 일으킵니다.
비용의 변화 $\Delta C$는 다음의 식에서와 같이 가중치에서의 변화 $\Delta w^l_{jk}$와 연관되어 있습니다.
$\begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial w^l_{jk}} \Delta w^l_{jk}.\tag{47}\end{eqnarray}$
이것은 $\frac {\partial C}{\partial w^l_{jk}}를 계산하는 방법이 $가중치 $w^l_{jk}$의 작은 변화가 어떻게 $C$에서의 변화로 이어지는지를 주의깊게 추적하는 것을 뜻합니다. 우리가 모든 것을 쉽게 계산할 수 있는 값으로 표현하고자 합니다. 그렇다면, 우리는 $\partial C / \partial w^l_{jk}$를 계산할 수 있어야 합니다.
자, 이것을 한번 계산해봅시다. 가중치의 변화 $\Delta w^l_{jk}$은 $l^{th}$ 계층의 $j^{th}$ 뉴런의 활성화에서 변화 $\Delta a^l_j$를 일으킵니다. 이 변화는 아래와 같습니다.
$\begin{eqnarray} \Delta a^l_j \approx \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk}.\tag{48}\end{eqnarray}$
이 활성화의 변화 $\Delta a^l_j$는 이후 계층, 즉 $(l + 1)^{th}$ 계층에서의 모든 활성화에 변화를 일으킵니다. 우리는 영향을 받는 활성화 중 단 하나, $a^{l+1}_j$에만 집중하도록 하겠습니다.
사실 이것은 다음과 같이 표현될 수 있습니다.
$\begin{eqnarray} \Delta a^{l+1}_q \approx \frac{\partial a^{l+1}_q}{\partial a^l_j} \Delta a^l_j.\tag{49}\end{eqnarray}$
식 (48)의 표현식을 대입하면, 우리는 다음을 얻을 수 있습니다.
$\begin{eqnarray} \Delta a^{l+1}_q \approx \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk}.\tag{50}\end{eqnarray}$
물론, $\Delta a^{l+1}_q$는 다음 계층의 활성화에 변화를 일으킵니다. 사실 우리는 $w^l_{jk}$로 부터 $C$까지, 활성화의 각 변화가 다음 활성화에 변화를 발생시키며 결국에는 출력 계층에서 비용 $C$의 변화로 이어지는, 신경망을 통해 전파되는 경로를 상상해볼 수 있습니다. 만약, 그 경로를 따라 출력 활성화가 $a^l_j, a^{l+1}_q, ..., a^{L-1}_n, a^L_m$과 같이 일어난다면, 비용의 변화는 다음과 같을 것입니다. (우리가 거쳐하는 모든 뉴런에서의 $\partial a / \partial a$과 같은 형태의 항목와 마지막에 $\partial C / \partial a^L_m$ 항목이 있습니다.)
$\begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk},\tag{51}\end{eqnarray}$
위의 식은 비용 $C$의 변화는 신경망의 특정 경로의 활성화의 변화에서 기인한다는 것을 의미합니다. 물론, 특정 가중치 $w^l_{jk}$의 변화가 전파되어 비용 $C$까지 영향을 미치는 많은 경로가 있습니다. 그리고, 우리는 긎그 중 단 하나만 살펴보았습니다. 비용 $C$에 대한 전체 변화를 계산하기 위하여, 우리는 변화가 일어나는 가중치에서 마지막 비용 $C$사이의 모든 가능한 경로에서 일어나는 변화를 다음과 같이 더해야 합니다.
$\begin{eqnarray} \Delta C \approx \sum_{mnp\ldots q} \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk},\tag{52}\end{eqnarray}$
위 식에서 우리는 경로에 있는 모든 중간 뉴런의 활성도를 모두 합산했습니다. 식 (47)과 비교해 보면 아래와 같습니다.
$\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = \sum_{mnp\ldots q} \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}}.\tag{53}\end{eqnarray}$
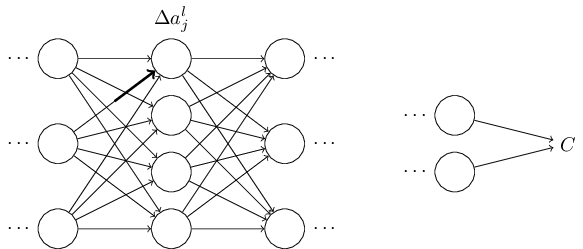
식 (53)은 꽤 복잡해 보입니다. 하지만, 직관적으로 해석하기 쉽습니다. 우리는 신경망의 가중치에 대한 $C$의 변화율을 계산하고 있습니다. 이 식은 신경망의 두 뉴런 사이의 모든 연결이 비율 인자와 연관되어 있다는 것을 의미하는데, 이는 비율 인자는 한 뉴런의 활성화를 다른 뉴런의 활성화에 대하여 편미분한 값입니다. 첫번째 뉴런으로의 연결은 $\partial a^l_j / \partial w^l_{jk}$의 비율 인자를 갖는다. (주: 첫번째 뉴런은 이전 뉴런으로부터의 변화가 없었으므로 활성화 비율 인자($\partial a / \partial a$)를 갖지 않고, 가중치와 활성화 비율 인자($\partial a / \partial w$)를 갖는다는 의미) 전체 경로에 대한 비율 인자는 경로를 따라 있는 모든 비율인자의 곱셈이 된다. $\partial C / \partial w^l_{jk}$의 변화에 대한 총 비율은 변화가 발생하는 초기 가중치에서 최종 비용 $C$까지의 모든 경로의 비율 인자의 합이다. 이 절차를 이해하기 위한 한 경로에 대한 그림은 아래와 같다.
지금까지 우리는 신경망에서 가중치가 변경되었을 때, 어떤 일이 일어나는지에 대한 논증을 해보았습니다. 이 논증을 더욱 발전시키는데 도움이 될 수 있는 한가지 방법을 간략히 설명해보겠습니다. 먼저 식 (53)의 모든 개별 편미분에 대한 명시적 식을 약간의 미적분학으로 유도할 수 있습니다. 그런 다음 모든 인덱스에 대한 합을 행렬 곱셈으로 산출할 수 있습니다. 이것은 약간의 끈기가 필요하지만 특별한 통찰력이 필요한 것은 아닙니다. 이 모든 것을 수행한 후 가능한 한 단순화하면 정확히 역전파 알고리즘을 얻게됩니다. 따라서, 역전파 알고리즘은 이러한 모든 경로에 대한 비율 인자에 대한 합을 계산하는 방법을 제공합니다. 약간 다르게 표현하면 역전파 알고리즘은 신경망을 통해 전파되어 출력ㅇ 도달하고 비용에 영향을 미치는 가중치(또는 편향)의 작은 변동을 추적하는 좋은 방법입니다.
자, 여기서 이 모든 것을 설명하지 않겠습니다. 복잡하고 모든 세부사항을 꼼꼼히 살펴보려면 상당한 주의가 필요합니다. 도전할 의향이 있으면 시도해 보는 것도 좋습니다. 설령 그렇지 않더라도 이러한 생각을 통해 역전파 알고리즘이 무엇을 하는지 조금이나마 이해할 수 있기를 바랍니다.
나머니 다른 미스터리는 무엇일까요? 역전파 이론이 당초 어떻게 발견될 수 있었을까요? 사실, 제가 방금 설명한 접근법에 따르면 이론의 증명을 발견할 수 있습니다. 안타깝게도 이 증명은 이 장의 앞부분에서 설명한 것보다 훨씬 길고 복잡합니다. 그렇다면 그 짧지만 더 신비로운 증명은 어떻게 발견되었을까요? 긴 증명의 모든 세부사항을 적어보면 나중에 몇가지 명백한 단순화가 눈앞에 있다는 것을 알게됩니다. 그 단순화들을 만들고 더 짧은 증명을 얻어서 적어보면, 몇 가지 더 명백한 단순화들이 눈에 띕니다. 그래서 다시 반복합니다. 몇 번의 반복 끝에 나온 결과가 앞서 보았던 증명입니다. 짧지만 다소 모호한 부분이 있습니다. 왜냐하면 이 증명의 구조를 설명하는 모든 이정표가 제거되었기 때문입니다. 물론, 이 부분은 믿어주시기 바랍니다. 하지만 앞서 제시된 증명의 기원에 대해 큰 미스터리는 없습니다. 이 부분에서 제가 간략하게 설명한 증명을 단순화하는데 많은 노력이 들었을 뿐입니다.










댓글 없음:
댓글 쓰기